
Photo by Alexander Sinn on Unsplash
Bit manipulation & bitwise operators
A Beginner's Guide to Bit Manipulation and Bitwise Operators
Let's dive right into bitwise operators. If you need to operate on numbers of other bases, you first have to convert them to binary.
You may come across different prefixes that denote different bases. It is supposed to tell you what base the number is, for appropriate conversion perhaps. Use this table for reference.
| prefix(notation) | base |
| 0b | 2 (binary) |
| 0x | 16 (hexadecimal) |
| 0o | 8 (octal) |
Binary Operators
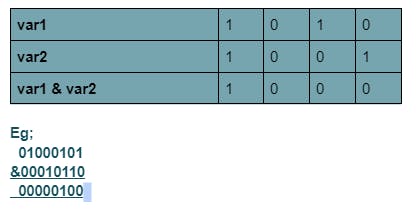
Bitwise AND (&)
It is a binary operator meaning it takes two numbers. It compares the operands bit by bit such that if both bits are 1 resulting bit is 1, otherwise, it is 0.
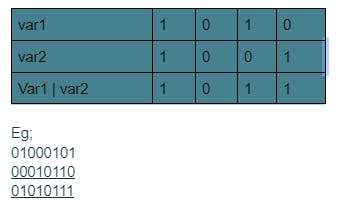
Bitwise OR ( | ) a.k.a Inclusive OR
It compares the operands bit by bit such that if both of them are 0, the resulting bit is 0. Otherwise, it is 1.
It can be used to set a bit at a given index to 1 , using a mask that has a 1 and that particular index.
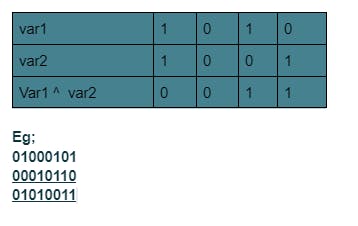
Bitwise XOR ( ^ ) a.k.a Exclusive OR
Basically, only when one of the bits is 1, is the resulting bit 1. Otherwise, it is 0. Refer to the table below.
Left Shift Operator (<< )
It takes two operands in this format;
A << n
On the left of the operator is the operand and on the right (n) is the number of places to shift left. Let's see it in action, shall we?
12 << 2
First, we convert 12 to binary, We get 00001100.
We then shift it 2 places to the left to get 001100_ _.
The trailing positions are filled with zeros so now we have 00110000
Lastly, we convert it back to whatever base it was in our case decimal (base 10).
12 << 2 = 48
As there are many ways to kill a mango, whatever they said. You can achieve the same result with a different formula.
A multiplied by 2 to power n
12 << 2 = 12 * 2^2 = 48
5 << 1 = 5 * 2^1 = 10
Right Shift Operator ( >> )
Here we shift to the right by truncating the operand by the number of places specified. Then we fill the leading position with zeros. Don't worry, I can explain.
A >> n
Step 1: We will use the same number 12 but right-shift it this time.
12 >> 2
We shift 00001100 2 places to the right so now we have _ _ 000011.
00000011 converted to decimal is 3.
12 >> 2 = 3
We also have a shortcut but here, we divide.
A >> n = A / 2^n
12 >> 2 = 12 / 2^2 = 3
Unary Operators
They take only one operand.
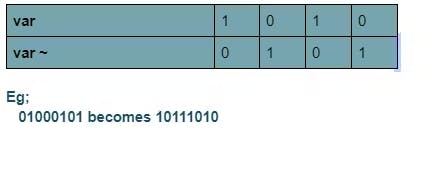
Bitwise NOT ( ~ )
This does an inverse of the digits in the operand. i.e 0 becomes 1 and vice versa.
Bit Manipulation
mask - a mask is a bit pattern that you can use to modify or compare specific bits in a larger data structure such as a byte
Least significant bit (LSB) - It's the bit that represents the smallest value in the number, or the bit with the lowest positional value. For example, in the binary number 10011010, the LSB is the rightmost bit, which has a positional value of 1.
Most Significant bit (MSB) - It's the bit that represents the largest value in the number, or the bit with the highest positional value. For example, in the binary number 1110, the MSB is the leftmost bit, which has a positional value of 8.
Swap bits
if you want to swap all the bits of a given number, use the bitwise XOR operator
a^=b
b^=a
a^=b
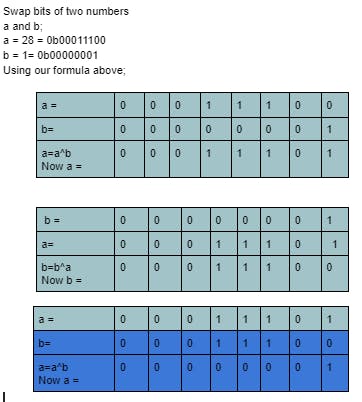
Finally, a is b and b is a.
set bit to 0
You can use bitwise AND for this operation, using a mask that has all 1s except for a 0 at the 3rd-bit position.
eg; if you have a number n and you want to set the 3rd bit to 0, you can AND n with a mask. Here's an example;
n = n & ~(1 << 2) where 1 is the mask, 00000001 in binary, and 2 left shifts the bits so we have 00000100.
Run it through bitwise NOT to have 11111011. Bitwise & sets all bits to zero unless it is a 1 & 1.
In our case, there's no chance the number at position 2 becomes one so it gets set to 0
Toggle / Invert bits
You use bitwise XOR to invert individual bits. Eg if you have a number n and want to invert the 3rd bit, you can XOR n with a mask that has all 0s except for a 1 at the 3rd-bit position. Here's an example
n = n ^ (1 << 2)
1 = 00000001, left shift it to get 00000100. If you run n ^ 00000100, there can only be two possibilities for the numbers at position 2
0 ^ 1 or 1 ^ 1 and if you recall how bitwise XOR operates, either way, an inversion happens to the bit at that position
Invert all bits of a number
You use bitwise NOT for this.
n = ~n
It is as simple as that. This inverts all 0s to 1s and vice versa.
I hope this has helped you. Have a code day!
